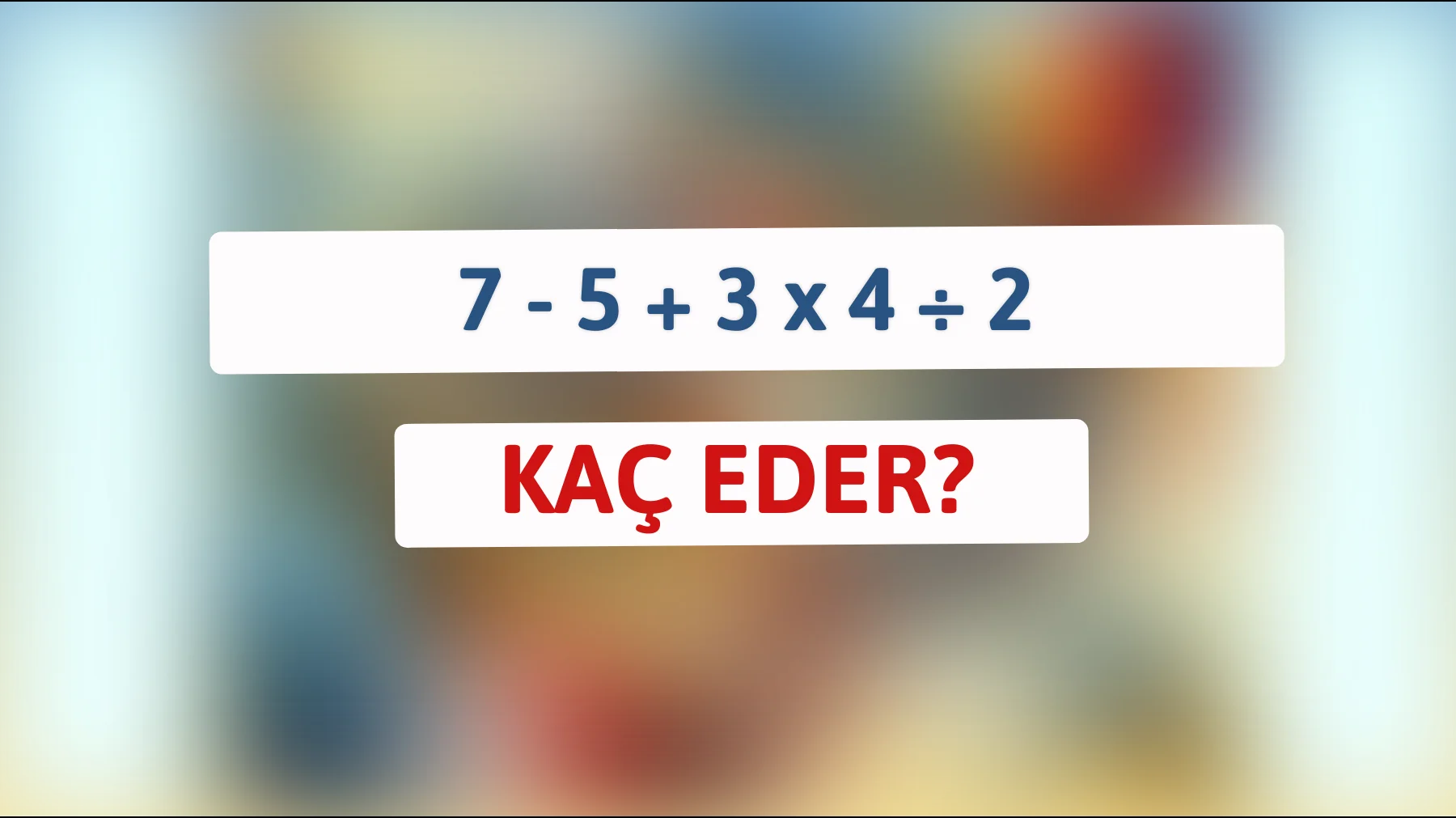Matematik bilmece dünyasında hoş bir meydan okumaya hazır mısınız? Kaç eder 7 – 5 + 3 x 4 ÷ 2 gibi bir işlem, matematik dünyasının keyifli bir labirenti gibidir. Her adımda hangi kuralı uygulayacağınıza karar vermek, zihinsel olarak uyanık kalmanın anahtarı olabilir. Bu tür bir bulmacaya nasıl yaklaşacağınızı öğrenmek, sadece doğru çözüme ulaşmanıza yardımcı olmakla kalmaz, aynı zamanda analitik düşünce yeteneklerinizi de geliştirir.
Karmaşık görünen bir matematik bulmacasıyla karşılaştığınızda, her adım için doğru sırayı bilmek kritik önem taşır. Matematikte, bu işlem sırasına uymak demek hata yapma olasılığınızı en aza indirebilir. Peki, kaç eder 7 – 5 + 3 x 4 ÷ 2 dediğinizde aklınıza gelen ilk adım nedir? İşlem yüzeyde basit görünebilir, ancak doğru bir sonuç elde etmek için belirli kurallara sadık kalmanız gerekir.
Öncelikle, ilk adımınızı belirleyin: Matematiksel operasyonlar arasında belirli bir hiyerarşi vardır. Öncelikli olarak çarpma ve bölme işlemleri gelir, ardından toplama ve çıkarma. Bu hiyerarşiye göre önce çarpma ve bölme işlemleri yapılır. Bu basit bir kural gibi görünse de sonuç üzerinde büyük bir fark yaratabilir. Unutmayın, detaylar önemlidir!
Matematik Problemleri ve Lateral Düşünme
Çarpma ve bölme ile başlamak, çözümün kilidini açmak için ilk adımdır. İlk olarak, işlemi ele alırken 3 x 4 hesaplanır, bu da bize 12’yi verir. Ardından 12 ÷ 2 işlemi yapılır ve sonuç 6’dır. Bu sayede problem, çok daha basit bir hale dönüşür: 7 – 5 + 6.
Şimdi, bu adımda toplama ve çıkarma işlemlerini sırayla ele alarak sonuca ulaşabilirsiniz. İlk olarak, 7 – 5 işlemi yapılır, sonucunda 2 elde edilir. Bu noktada işlemin son adımı, yani toplama işlemi devreye girer. 2 + 6 hesaplanır ve nihai sonuç 8 olarak bulunur. Akılda tutulması gereken şey, işlem sırasına bağlı kalarak her adımda dikkatli olmanız gerektiğidir. Bu işlemle birlikte, matematik problemlerinin karmaşıklığının üstesinden gelmenin yolunu keşfetmiş oldunuz!
İşlem Sırası ve Anahtar Matematik Terasyonları
Şimdi ilginç bir matematiksel detayla karşınızdayız: Örneğimizin çözüm sayısı olan 11, başlı başına dikkat çekici özelliklere sahip. **11**, bir asal sayı olarak matematik dünyasında özel bir yer tutar. Aynı zamanda, bu sayı asal sayı ikizleri olarak bilinen bir fenomenin parçasıdır çünkü **11** ve **13** ardışık iki asal sayıdır. Asal sayıların büyüleyici dünyası, matematik severler için ilginç bir alan olmaya devam etmektedir. Bu da, sıradan bir işlem sonucunun dahi ne kadar derin ve sürükleyici bilgi katmanları barındırabileceğinin bir kanıtıdır.