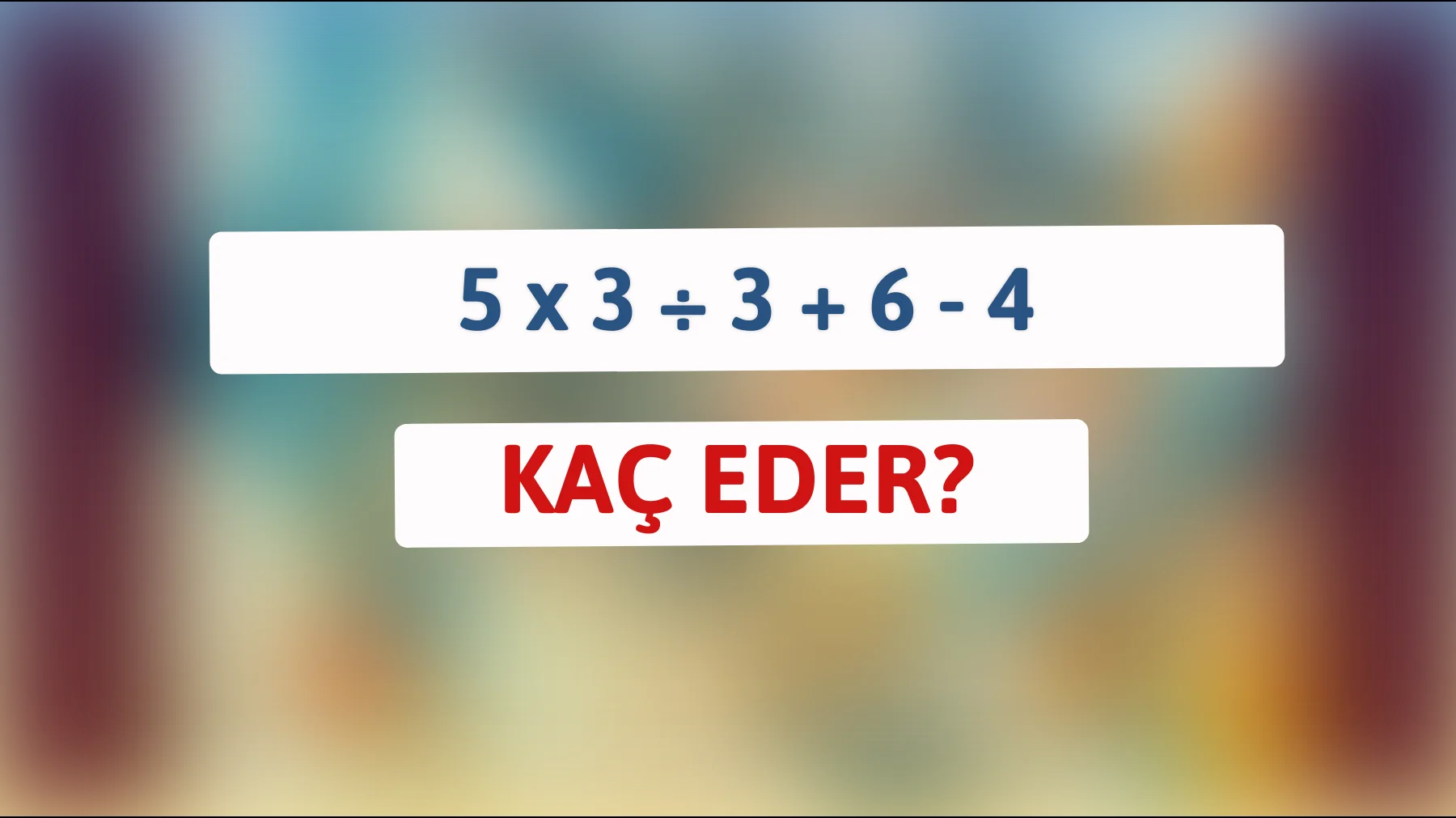Günlük yaşamın içerisinde belki de farkında olmadan sık sık kullandığımız, ancak derinlerine indikçe gizemli ve bir o kadar da düşündürücü hale gelen matematik işlemlerine bir göz atalım. Karşınızda: 5 x 3 ÷ 3 + 6 – 4. Bu sıradan gibi görünen ifadede gizli olan çözümü ve matematiğin karmaşık olduğu kadar büyüleyici dünyasına adım atmaya hazır mısınız?
Bu matematik bilmecesi, ilk bakışta basit gibi görünse de birçok kişinin işlem sırasını karıştırmasıyla karmaşık hale gelebiliyor. Birçok öğrenci, bu tür işlemlerde hangi sıranın takip edileceği konusunda kafa karışıklığı yaşayabilir. Ancak aslında bu, temel bir işlem pratiği ve doğru sıra bilgisiyle kolaylıkla çözülebilir. Peki, bu ifade neden bu kadar kafa karıştırıcı? Çarpma, bölme, toplama ve çıkarma arasında kaybolmamak için biraz daha detaya inelim.
Öncelikle, matematik işlemleri çözümlerken dikkat etmemiz gereken en önemli şey işlem sırasıdır. Bu işlem sırası, matematiğin dili olan denklemlerin doğru okunup anlaşılması için gereklidir. İşte bu yüzden “önce hangi işlem yapılır” sorusu, bu tür bilmeceler karşısında en çok kendine yer bulan sorulardan biridir. Eğer kafanız karışık halde bu sorunun cevabını arıyorsanız, doğru yerdesiniz. Şimdi bu işlemin derinliklerine inerek sırrını birlikte çözelim.
Çarpma ve Bölmenin Önemi: Matematiğin Gizemli Dünyası
İlk adım çarpma işlemi: 5 x 3. Bu basit adım, 15 rakamını karşımıza çıkarıyor. Çarpma işlemi her zaman kendini güçlü hissettirir çünkü değerleri hızla artırır. Bu noktada, elde ettiğimiz 15 ile yolculuğumuz devam ediyor. Ancak hala pek çok kişi bu adımdan sonra hangi işlemi yapacağını karıştırıyor olabilir.
Şimdi sırada bölme işlemi var: 15 ÷ 3. Burada, çarpma işlemiyle güçlenen sayıyı bölme işlemiyle tekrar sadeleştiriyoruz. Bu sadeleştirme, matematin büyülü dengesini korur ve elimizde daha az karmaşık bir 5 değeri bırakır. Böylece zihin, işlemler arasında gezinirken bir nebze soluklanabilir. Bu iki adımın önemini kavramak, matematik bilmecelerinin kilidini açıyor ve içindeki hazineyi gün yüzüne çıkarıyor.
TOPLAMA VE ÇIKARMANIN DANS ETTİĞİ AN: SEVİLEN YEDİYE ULAŞMAK
Şimdi daha huzurlu bir şekilde toplama işlemine geçebiliriz. Bu noktada elde ettiğimiz 5 sayısının değerine, 6 ekleyerek toplamda 11’e ulaşıyoruz. Toplama işlemiyle sayılar arasında kurduğumuz bu bağ, çıkarma işlemiyle zıt kutuplara taşınıyor. Bundan sonrasında ise basit bir çıkarma: 11 – 4. İşte bu son adıma geliyoruz ve sonunda sonucu buluyoruz: 7.
Her adımın önemini anlamak ve işlemleri sırayla çözmek, bizi gizemli dünyaların kapılarından geçirir. **7** ile tanıştınız; 7, sadece problemleri çözmez, aynı zamanda matematik tarihinde birçok kültürde şanslı bir sayı olarak kabul edilir. Aynı zamanda asal bir sayıdır, yani sadece 1 ve kendisiyle bölünebilir. Bu da onu matematiksel olarak özel kılar. Matematiğin büyüsüne kapılmak için eşsiz bir fırsat. Görev tamamlandığında, zihin biraz daha keskin ve matematiği biraz daha sevgi doludur. Bir dahaki sefer bir matematik bilmeceyle karşılaştığınızda, artık biraz daha cesur olabilirsiniz.