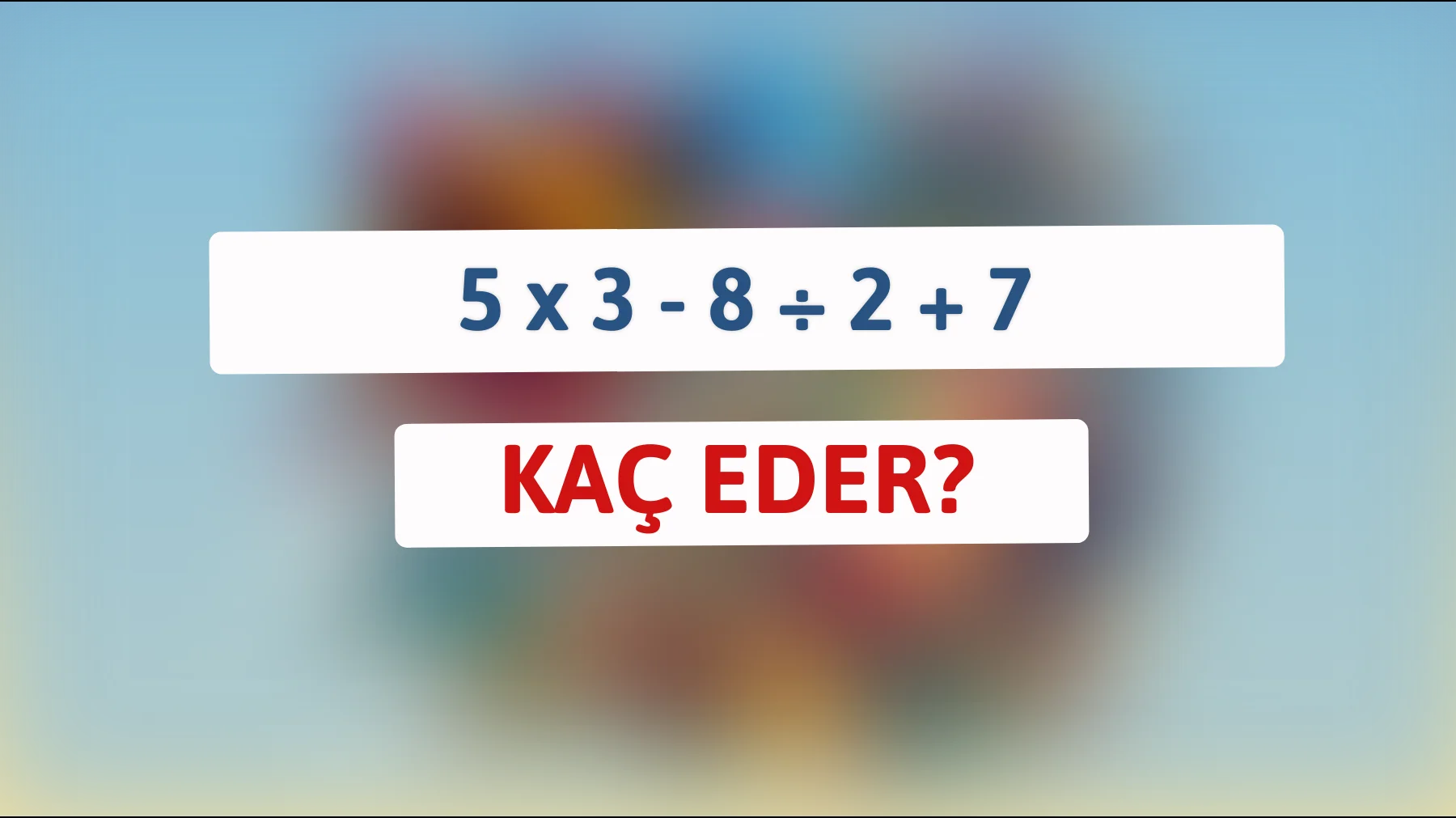Hesaplayınca ne olur dersiniz? Basit bir matematik işlemi gibi görünen bu problem, aslında dikkat edilmediğinde karmaşık bir hal alabilir. 5 x 3 – 8 ÷ 2 + 7 işlemini çözmeye hazırsanız, işlem sırasının neden bu kadar önemli olduğunu birlikte keşfedelim!
Her gündelik hayatımızda karşılaştığımız problemlerle başa çıkmak için matematiği kullanırız; ancak bazen en basit görünen işlemler bile dikkatimizi yeterince vermediğimizde bizi yanıltabilir. Bu matematik problemini çözmeye çalışırken, doğru şekilde yapılmayan sıradan bir hata sonucu tamamen yanlış bir cevaba ulaşmak mümkün. 5 x 3 – 8 ÷ 2 + 7 gibi bir işlemi sadece sol baştan çözmeye çalışırsanız, büyük bir yanılgıya düşebilirsiniz.
İşlem sırasına dikkat ederek çözüme ulaşabiliriz. İlk olarak yapılması gereken, çarpma ve bölme işlemlerini öne almaktır. Bu durumda, öncelikle 5 x 3 ve ardından 8 ÷ 2 hesaplanmalıdır. Çarpma işleminde 5 ve 3 çarpılarak 15 elde edilir. Sonrasında, 8 ÷ 2 işlemi yapılır ve sonuç 4 olarak bulunur.
Basit Matematik Problemleri İçin İşlem Sırası Neden Önemlidir?
İşlem sırasının önemini kavradığımıza göre, gelin bu kuralların arka planını inceleyelim. Matematikte işlem sırası, **Parantez, Üs, Çarpma, Bölme, Toplama, Çıkarma** (PEMDAS veya BODMAS) kısaltmalarıyla bilinir. Matematikte çarpma ve bölme işlemleri aynı aşamada yer aldığı için, problemde hangisi önce geliyorsa o işlem yapılır. Aynı durum toplama ve çıkarma için de geçerlidir.
Bu durumda yaptığımız işlem doğru şekilde sıralandığında, başlangıçta 5 x 3 ve 8 ÷ 2 işlemleri tamamlanmış olur. Sonrasında, kalan işlemleri toplama ve çıkarma sırasıyla çözmek bize kesin sonucu verecektir. Bu örnekte, **15 – 4** işlemi yapıldıktan sonra 11 elde edilir, ardından **11 + 7** şeklindeki toplama işlemini gerçekleştirerek nihai sonuç 18 olarak bulunur.
İşlem Sırası Kullanarak Karmaşık Problemleri Kolayca Çözmek
Analitik düşünmenin yanı sıra, matematikteki işlem sırasını öğrenmek, daha karmaşık problemlerde hata yapmanızı engelleyecek önemli bir adımdır. 5 x 3 – 8 ÷ 2 + 7 işleminin sonucuna ulaştığımızda 18 gibi basit bir sayı elde ederiz; fakat bu bir son değil. 18 sayısı aslında pek çok matematiksel özelliğe sahiptir. Örneğin, ardışık iki kare sayının toplamı olarak da ifade edilebilir: 3² + 3² = 9 + 9 = 18. Ayrıca, 18, 1’den 18’e kadar olan sayıların toplamı olan 171’in bir üçgensel sayı temsilidir.
Gördüğünüz gibi, basit bir işlemin altındaki matematiksel özellikler bize geniş bir düşünce alanı sunar. Matematik problemlerinin sadece doğru sayıyı bulmakla bitmediğini, derin düşünce ve analizle çok daha fazlasını anlamamıza yardımcı olduklarını unutmamalıyız. İşte burada, **işlem sırası** ve analitik düşünce devreye girer. Dolayısıyla bir sonraki matematik probleminde, bu prensipleri hatırlayın ve basit gibi görünen her problemin ardında sizi bekleyen bir dünya olduğunu unutmayın!