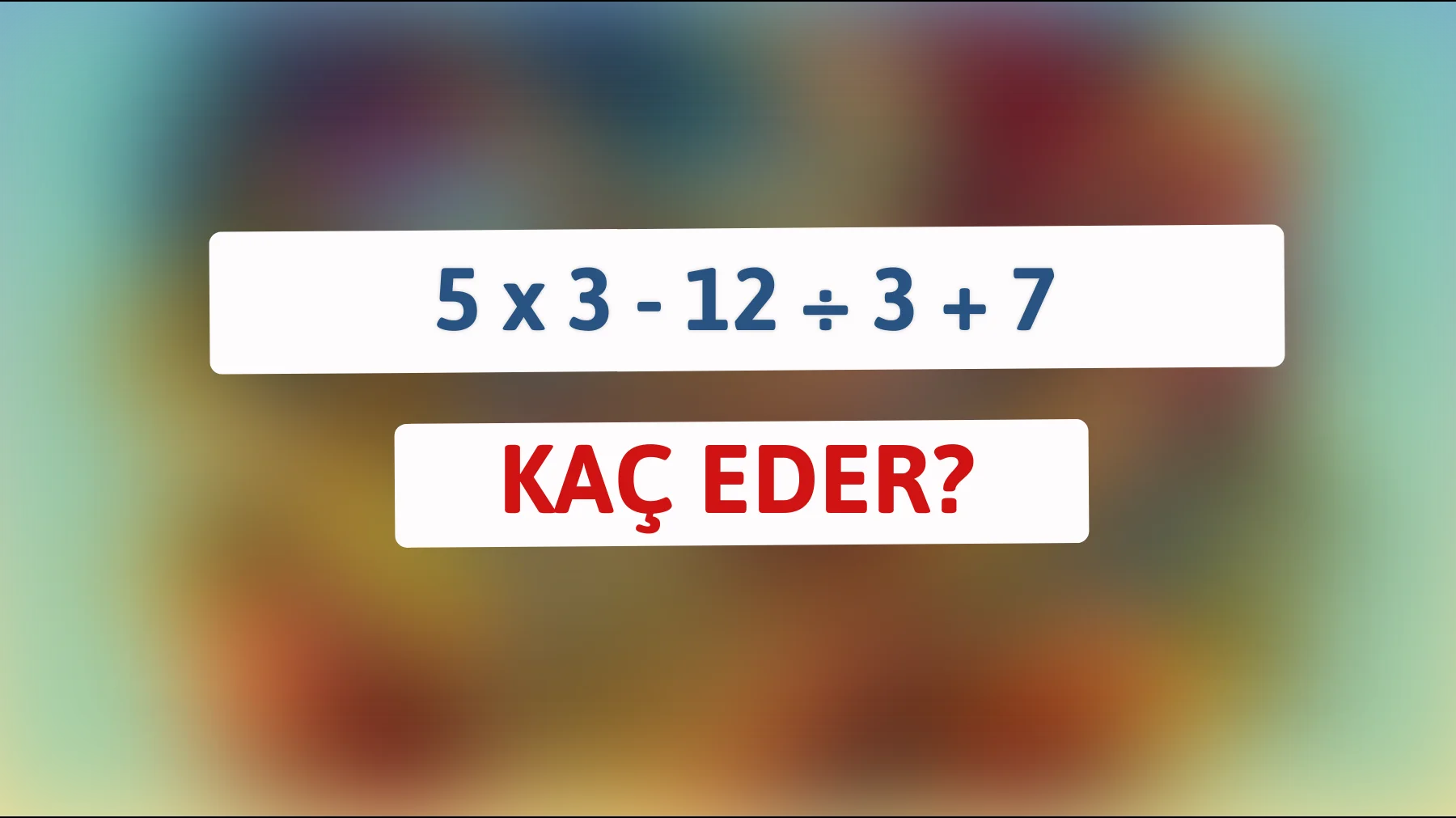Matematik, beyinde kıvrımlar yaratan ve her doğru yanıtta içimizi kıpır kıpır eden bir evrendir. İşte bu evrende sizi kısa bir yolculuğa çıkarmaya davet ediyoruz: 5 x 3 – 12 ÷ 3 + 7 işlemi! Sizce sonuç nedir?
Matematik problemleri çözmek, beynimizi dinç tutmanın en etkili yollarından biridir. Her bir adımda mantıklı bir zeka oyunu oynar ve beynimizin derinliklerine işleyen sofistike problem çözme yeteneğimizi geliştiririz. İster okulda olsun, isterse günlük hayatta, matematikle her zaman karşı karşıyayız. Ancak bu sefer klasik bir problemle değil, oldukça ilginç bir matematiksel denklemle karşı karşıyayız. “5 x 3 – 12 ÷ 3 + 7” işte bizi bekleyen meydan okuma bu!
Bu işlemi çözerken detaylara dikkat etmek büyük önem taşıyor. İnanması güç olabilir ama, hatalı bir sırayla işlem yaparak kendimizi kolayca yanlış bir sonuç bulabilme tehlikesine düşürebiliriz. Unutmayın, burada anahtar nokta işlemler arası öncelik sırasını doğru belirlemek. Denklemlerdeki bu oldukça temel ama hayati kuralı unuttuğunuz anda sonuçlar ansızın beklentilerinizi altüst edebilir.
Matematiksel İşlemlerde Öncelik Sırası ve Zorluklar
Her işlemde olduğu gibi burada da önce çarpma ve bölmelerden başlamalıyız. Öncelikle 5 x 3 işlemini ele alarak ilk çarpım sonucunu elde ediyoruz. **Sonuç: 15.** Ardından bölme işlemi geliyor, burada 12 ÷ 3 işlemiyle karşı karşıyayız. **Sonuç: 4.** Artık elimizde daha basit bir denklem var: 15 – 4 + 7. İşte şimdi toplama ve çıkarmalar geliyor. İlk olarak çıkarma işlemi: 15 – 4. **Sonuç: 11.** Ve en sonunda toplama işlemine geçiyoruz: 11 + 7. İşte cevabımız burada saklı: **18.**
Bu işlem adımlarını dikkatlice takip etmek, doğru cevaba ulaşmanın anahtarıdır. Bunun yanı sıra, bu mantık zinciri aynı zamanda günlük sorunları analiz edip çözme yeteneğimizi de geliştirmemize yardımcı olur. Çarpma ve bölme işlemlerini öne çıkarmak, düşünme süreçlerimizde odaklanmayı ve stratejik planlamayı teşvik eder.
İlginç Matematiksel Bilgiler ve 18 Sayısının Önemi
18 sayısı üzerinde düşünürken, matematiğin sadece sayılardan ibaret olmadığını, aynı zamanda estetik ve ilginç ilişkilerle dolu olduğunu fark ederiz. Örneğin, 18, dokuzuncu Fibonacci sayısının iki katıdır. Fibonacci dizisi ise, doğada kendini sıkça gösteren harika bir sayı dizisidir ve her sayının, önceki iki sayının toplamı olduğu bu dizide 18’in bulunduğu konum da oldukça özeldir. Ayrıca, ilk dört doğal sayının çarpımının sonucunda bulduğumuz sayı olan 24 eksildiğinde, elimizde kalan ilginç sonuç yine 18’dir.
Bu tür bilgiler matematiksel problemlerde başarımızı kuvvetlendirirken, aynı zamanda sayılarla sanat yapmanın mümkün olduğunu gösterir. Matematiği sadece basit bir hesaplama aracı olarak görmek yerine, bu tür derin anlamlar arayan ve bulan bir keşif yolculuğu olarak görmeyi seçtiğimizde, bakış açımızı genişletiriz. Sonuç olarak, “Kaç eder 5 x 3 – 12 ÷ 3 + 7?” gibi basit görünen bir sorunun bile bizi ne denli zenginleştirebileceğini ve zihinsel sınırlarımızı nasıl zorlayabileceğini hiç unutmamalıyız.